1.5 PADRÕES E RELAÇÕES NUMÉRICAS

Sabe-se que Pitágoras passou a vida fazendo conferências sobre números e figuras e com seus alunos formavam uma sociedade secreta que cobria a matemática de grandes mistérios.

As descobertas matemáticas eram conservadas tão em segredo que no século IV antes de Cristo, conta a lenda que, Hipassus, membro de uma dessas sociedades foi afogado no mar por ter transmitido a um leigo algumas verdades matemáticas.

Pitágoras colocou qualidades morais nos números e nas figuras. O um representava a razão, o dois representava a opinião, o quatro a justiça, o cinco, o matrimônio, pois era a fusão do três o primeiro número macho com o dois, o primeiro número fêmea.

Na videoteca da TV Escola encontramos o vídeo “O Legado de Pitágoras- Pitágoras e outros”, vale a pena assistir, http://tvescola.mec.gov.br

Haviam os números perfeitos, cujos divisores (diferentes do próprio número), se somados, reproduziam o próprio número. O primeiro era o 6, cujos divisores (diferentes de 6) são 1 , 2 e 3 , o segundo o 28, o terceiro 496 e o quarto 8128.

Vamos mostrar que o 28 também é perfeito e você deve mostrar que 496 também o é.

Os divisores de 28, distintos de 28 são: 1, 2, 4, 7 e 14. E por sua vez

Na época de Pitágoras ainda se contava através do uso de marcas e os pitagóricos eram observadores das formas geométricas. Daí a sua atenção para os números figurados. Estes como o próprio nome diz, resultam de arranjos com pontos de maneira a formar figuras geométricas como triângulos, quadrados, pentágonos, hexágonos.

Os números triangulares são formados acrescentando-se a um número, todos os seus precedentes. Como representado no desenho.

Há uma história acerca dos números triangulares, que mostra como a matemática deixava aos poucos de ser um instrumento à disposição dos comerciantes e artífices, para se transformar num conhecimento hermético, ou de mera recreação espiritual. Um comerciante pergunta a Pitágoras o que este lhes pode ensinar.

- “Ensinar-te-ei a contar” - responde Pitágoras.

– “Contar já sei...” - fala o comerciante.

- “E como conta tu?” – pergunta o filósofo.

E o comerciante começa:

- “Um, dois, três, quatro,...”

- “Pára!” - diz Pitágoras.

- “O que tomas por quatro é dez, o triângulo perfeito, o nosso símbolo!...”

EXEMPLO 5.1

Números Triangulares

Vamos determinar quantos pontos tem a figura . Observemos que cada número triangular, a partir de é obtido do anterior somando 2, 3, 4, 5, etc. pontos ao número triangular anterior.

é obtido somando 4 ao e tem tem 10 pontos

É fácil ver que tem 15 pontos. Observe o que faremos para obter o número de pontos do número triangular

.

e o número triangular tem 5.050 pontos, vejamos

Trocando a ordem das parcelas

somando:

.

O que fizemos foi somar duas vezes as 100 parcelas de .

De um modo geral, fazendo o mesmo para a figura

para

isto significa que

EXEMPLO 5.2 Números Quadrados

Todo número ímpar pode ser escrito na forma 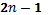. Ou na forma , como pode ser observado na Tabela 5.1

Tabela 5.1

n	2n-1	2n+1
0		1
1	1	3
2	3	5
3	5	7
4	7	9
5	9	11
...	...	...
100	199	201
...	...	...

Tem sentido essa expressão para os números ímpares, já que é par, para todo número natural n. O anterior a ele que é o 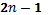é ímpar, assim como o seu posterior que é também é ímpar.

Voltando aos números quadrados

.

Encontr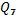e e .

Observando a expressão d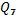e , e , notamos que

E concluímos que para todo número natural n, o n-ésimo número quadrado é:

.

Observação:

A frase acima “e concluímos que para todo número natural n” é muito forte, muito rápida, no sentido de garantir que se uma afirmação é verdadeira para os números etc. seja verdadeira para todo número natural, por exemplo para o número ou para o número .

Podemos afirmar que a soma dos números ímpares:

ela é verdadeira para todo número natural n. Se fôssemos pelo rigor da matemática deveríamos provar a veracidade da igualdade, teríamos que provar que a igualdade é realmente verdadeira. Existe, nas regras da matemática, um método conhecido como Método da Indução Finita, com esse método conseguimos provar afirmações do tipo: para todo número natural. Para o momento fica apenas como observação.

EXEMPLO 5.3

Números Pentagonais

Vamos fazer um desenho ilustrativo.

e

somando as duas igualdades

agora vamos encontrar

e para todo número natural n ,

EXEMPLO 5.4

Números Hexagonais

Apresentamos a figura e a expressão geral para 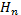, efetue os cálculos como no exemplo anterior.

Para todo número natural n: