1.8 RESOLUÇÃO DE PROBLEMAS

No dia 20 de julho de 1969, muitos curiosos, estudiosos e pesquisadores acompanharam pela televisão a grande aventura do século passado: a chegada do homem à Lua, na nave espacial Apolo 11. Este fato teve como protagonista principal o astronauta americano Neil Armstrong, engenheiro e piloto de provas. No mundo em 1969 ainda faltavam televisores, não havia computadores domésticos, nem se sonhava com algo como a Internet. No entanto, muitos dos equipamentos criados para os programas espaciais foram convertidos para a utilização no cotidiano das pessoas. De acordo com a NASA, mais de 30 mil aplicações secundárias surgiram de suas pesquisas em laboratórios desde 1958. Com certeza você está perguntando: o que a resolução de problemas em matemática tem a ver com programas espaciais e com aplicações secundárias? Encontramos respostas a esta pergunta quando analisamos os recentes desenvolvimentos das telecomunicações, da nanotecnologia, da medicina no nosso cotidiano e a definição de problema.

A partir dos anos oitenta a resolução de problemas torna-se recomendação nos modelos pedagógicos do mundo e é desnecessário justificar a sua importância na área de matemática.

Para a definição clássica de problema temos: uma situação que um indivíduo ou grupo quer resolver e para o qual não dispõe de procedimentos automáticos que permita solucioná-la de forma mais ou menos imediata. Já um exercício dispõe e utiliza mecanismos que levam quase que de forma imediata à solução.

A realização de exercícios se baseia no uso de habilidades ou técnicas transformadas em rotinas como conseqüência de uma prática contínua. A solução de problemas exige o uso de estratégias, a tomada de decisões sobre o processo de resolução a ser seguido.

A resolução de problemas e a realização de exercícios se completam para o aprendizado da matemática. Na resolução de problemas as técnicas previamente exercitadas, constituem um meio ou recurso necessário, mas não suficiente, para alcançar a solução; além delas são exigidas estratégias, conhecimentos matemáticos, atitudes, etc..

Para resolver um problema temos que:

1.      Compreender o problema,

2.      Conceber um plano que nos conduza à meta,

3.      Executar esse plano e, finalmente

4.      Analisar se alcançamos ou não essa meta.

Esta seqüência que acabamos de descrever é a que o matemático Polya estabelecia como necessária para a resolução de problemas.

Os quatro passos enumerados por Polya são hoje resumidos em dois grandes processos: tradução e solução do problema que são colocados em ação quando solucionamos algum problema.

O primeiro passo na resolução do problema consiste então na tradução das palavras, ou seja, transformação no formato de apresentação do problema para símbolos e representações matemáticas. Para a compreensão de um problema matemático são necessários conhecimentos da língua materna que facilitam a compreensão da tarefa, permitindo a sua representação em termos matemáticos que ajudam a elaborar um plano para resolvê-lo.

O processo de solução propriamente dito exige um conhecimento estratégico que nos ajuda a estabelecer as metas e os meios úteis para alcançá-las e um conhecimento operacional ou algorítmico que nos permite executar essas estratégias e planos.

Não existem procedimentos que ensinam a resolver problemas. No entanto algumas orientações podem ajudar:

a)      Expressar o problema com outras palavras;

b)      Explicar para alguém em que consiste o problema;

c)      Representar o problema com outro formato (gráficos, diagramas, desenhos, etc.);

d)     Indicar qual é a meta do problema;

e)      Apontar onde reside a dificuldade da tarefa;

f)       Separar os dados relevantes dos não relevantes;

g)      Indicar os dados com os quais contamos para resolver a tarefa;

h)      Indicar quais os dados que não estão presentes, mas que são necessários para resolver a tarefa;

i)        Procurar um problema semelhante que já tenhamos resolvido;

j)        Analisar inicialmente alguns exemplos concretos, quando o problema é muito geral.

O processo de solução de um problema termina quando o objetivo estabelecido foi alcançado e com a análise da solução obtida.

Lembramos que só aprendemos resolver problemas resolvendo-os e para isso necessitamos de persistência e força de vontade.

Vamos fazer alguns exemplos.

PROBLEMA 8.1

De um reservatório cheio de água, retira-se metade do seu conteúdo. A seguir, retira-se um terço do que restou e continua-se com esse processo. Na terceira vez retira-se um quarto do que restou, etc. Após quantas retiradas ficamos exatamente com um décimo da quantidade original?

Solução:

Este problema já possui uma linguagem matemática, não é necessário mudar a sua linguagem.

Vamos começar pensando na primeira retirada. Retiramos metade da água do reservatório, quanto sobra? Usando frações, sobra .

Na segunda retirada, da quantidade que sobrou, retiramos . Se retiramos de , sobraram 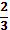de .

Como , na terceira retirada retiramos . Deverá sobrar .

Dando continuidade á solução do problema, podemos fazer figuras do reservatório nas sucessivas retiradas ou tentar uma tabela o que acho mais próprio. O que seria representar o problema em outro formato.

Primeira retirada	Retira	Sobra
Segunda retirada	Retira	Sobra
Terceira retirada	Retira	Sobra
Quarta retirada	Retira	Sobra
...	...	...
Nona retirada	Retira	Sobra

Se a pergunta do problema é: após quantas retiradas ficamos com um décimo da quantidade original de água? Depois da nona retirada ficamos com do conteúdo original.

A resposta está correta?

PROBLEMA 8.2

Pintam-se de preto todas as faces de um cubo de madeira cujas arestas medem 10 centímetros. Por cortes paralelos às faces, o cubo é dividido em mil cubos pequenos, cada um com arestas medindo 1 centímetro. Determine:

   1)     O número de cubos que não possuem nenhuma face pintada de preto.

   2)     O número de cubos que possuem uma única face pintada de preto.

   3)     O número de cubos que possuem exatamente duas faces pintadas de preto.

   4)     O número de cubos que possuem três faces pintadas de preto.

Solução:

Caso seja difícil a visualização do problema, use o cubo maior do “Material Dourado”.

Material Dourado

1)     Estão sem nenhuma face pintada, os cubos interiores ao cubo maior. Devem ser retirados todos os cubos que formam “a casca” do cubo maior, ficando assim um cubo de aresta 8. Esse cubo de aresta 8 possui cubos pequenos.

1)     2) Estão com uma face pintada aqueles que pertencem a uma face, mas não possuem lado comum com a aresta do cubo maior, isto é, cubos pequenos em cada face. Como são seis faces, temos cubos pequenos.

      3)     Para que um cubo tenha somente duas faces pintadas, ele deverá estar nas arestas, mas não nos vértices do cubo maior. Como são 12 arestas, teremos cubos pequenos.

     4)     Estarão com as três faces pintadas de preto aqueles que estão nos vértices, ou seja, 8 cubos pequenos.

Para verificarmos as respostas podemos fazer a recontagem no cubo do Material Dourado.

PROBLEMA 8.3

Qual é o algarismo das unidades do número ?

Solução

Podemos usar uma calculadora para descobrir alguma regra, não faz sentido tentar efetuar o cálculo, o número “não cabe” no visor da calculadora.

Observamos que:

e assim sucessivamente.

Podemos concluir que:

3 elevado às potencias 0, 4, 8, 12, ... termina em 1

3 elevado às potencias 1, 5, 9, 13, ... termina em 3

3 elevado às potencias 2, 6, 10, 14, ... termina em 9

3 elevado às potencias 3, 7, 11, 15, ... termina em 7

Já vimos este raciocínio quando trabalhamos com congruência: 0, 1, 2, e 3. São os possíveis restos na divisão por 4.

O número 2001 quando dividido por 4 deixa resto 1

se termina em 1 , termina em 3

PROBLEMA 8.4 (FUVEST)

Um número natural N tem três algarismos. Quando dele subtraímos 396 resulta o número que é obtido invertendo-se a ordem dos algarismos de N. Se, além disso, a soma do algarismo das centenas e do algarismo das unidades de N é igual a 8, então o algarismo das centenas de N é

a)      4

b)     5

c)      6

d)     7

e)      8

Solução

O que pede o problema?

Se o número tem três algarismos, , o problema pede o dígito a . Vamos entender o que foi dado para podermos encontrar o valor de a.

Quando escrevemos que , queremos dizer que . Temos também que: quando dele subtraímos 396 resulta o número que é obtido invertendo-se a ordem dos algarismos de N

Ao invés de trabalharmos com a diferença, fica muito mais simples trabalharmos com a adição

Para efetuarmos essa conta, precisamos escrever como:

logo

podemos simplificar, dividindo por 99 a igualdade

o problema nos dá mais uma condição que não usamos ainda: a soma do algarismo das centenas e do algarismo das unidades de N é igual a 8

se temos que .

Logo,

se encontramos , não importando o valor de b

Quando dizemos, não importando o valor de b, estamos afirmando que b pode valer de 0 até 9. Verifique essa afirmação.

O algarismo da centena é 6. A resposta correta é a letra c).

PROBLEMA 8.5 (OBMEP)

Quais números naturais m e n satisfazem a ?

Solução

Transformando a soma em diferença de modo que de um da igualdade só apareça a potência de 2

Comparando, temos que e são potencias de 2. A única solução possível é

e

resolvendo, obtemos .

Conseqüentemente e, obtemos .

PROBLEMA 8.6 (OBMEP)

Uma loja distribui 9999 cartões entre seus clientes. Cada um dos cartões possui um número de quatro algarismos, entre 0001 e 9999. Se a soma dos primeiros 2 algarismos for igual à soma dos 2 últimos, o cartão é premiado. Por exemplo, o cartão 0743 é premiado. Prove que a soma dos números de todos os cartões premiados é divisível por 101.

Observemos que se o cartão abcd é premiado então o cartão cdab também é premiado, por exemplo: 2341 e 4123 são ambos premiados. Assim sempre que temos dois cartões premiados cuja soma é

,

assim a soma desses dois cartões é divisível por 101.

No caso do cartão ser da forma

O número do cartão é divisível por 101. Assim a soma de todos os cartões é divisível por 101 já que a soma pode ser feita agrupando cartões do tipo abcd com cdab.

PROBLEMA 8.7 (OBMEP)

Um menino tentou alinhar 480 latas em forma de um triângulo com uma lata na primeira linha, 2 latas na segunda e assim por diante. No fim sobraram 15 latas. Quantas linhas têm esse triângulo?

Solução

Suponhamos que o triângulo está composto por n linhas, logo foram usadas latas, assim

se o produto de dois números naturais consecutivos é 930, o menor deles é 30. Concluímos que o triângulo tem 30 linhas.

Outro modo de escrever a equação é:

resolvendo a equação, obtemos:

ou .

Assim, 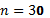é a solução positiva desta equação. Portanto o triângulo tem 30 linhas.